
WSZYSTKO O FRAKTALACH
Fraktal - definicja
Samo słowo fraktal (z łac. fractus - złamany, cząstkowy, ułamkowy) zostało wprowadzone w książce ,,The Fractal Geometry of Nature" przez Benoita Mandelbrota. Jest to pojęcie dość młode, gdyż Mandelbrot zdefiniował je w latach siedemdziesiątych XX w.. Odkryty przez Mandelborta zbiór nie był pierwszym takim zbiorem, już w wieku XIX mieliśmy do czynienia z obiektami geometrycznymi takimi jak: krzywa von Kocha czy dywanem Sierpińskiego.


Mandelbort w pierwszych pracach scharakteryzował fraktale trzema własnościami:
* są określone zależnością rekurencyjną, a nie wzorem;
* ich część jest podobna do całości, co oznaczam, że mają one cechy samopodobieństwa;
* ich wymiar nie jest liczbą całkowitą;
Celem Mandelborta było udowodnienie poglądu, że w naturze wszystkie obiekty mają strukturę fraktalną. Natomiast takie idealne twory jak linia prosta, kwadrat czy koło, są wymyślonym przez człowieka ,,uproszczeniem natury".
Wymienione własności nie są wystarczające, by być podstawą ścisłej definicji matematycznej.
fraktale
Czym jest fraktal?
Wiemy już jakie są własności fraktali, ale czym one tak naprawdę są?
Otóż są to figury samo podobne, oznacza to, że fraktal jest figurą, w której część figury jest podobna do jej całości;
Poniżej przedstawiam jak p[powstają niektóre fraktale:
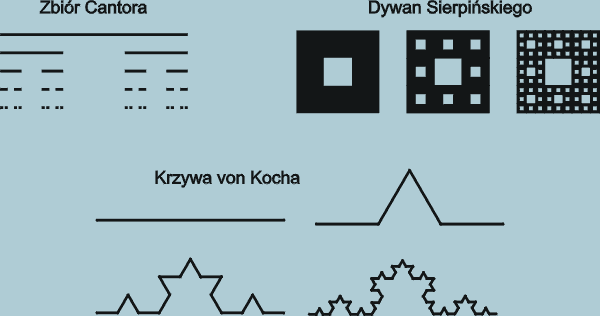


Przykłady fraktali:
Zbiór Cantora:

Jest to odcinek domknięty [0,1], podzielony na trzy równe części, z usuniętym odcinkiem środkowym (1/3, 2/3), pozostają tylko punkty brzegowe. Tę samą czynność powtarzamy z powstałymi dwoma odcinkami, w wyniku czego powstają cztery odcinki, z którymi robimy dokładnie to samo. Działania te prowadzą do powstania zbioru Cantora, który ukazuje powyższy obraz. Jest to zbiór zamknięty. Liczba jego punktów jest nieprzeliczalna oraz nie zawiera żadnego odcinka.
Krzywa von Kocha


Krzywa von Kocha jest opisywana jako granica ciągu linii łamanych. Pierwsze trzy kroki (0,1,2) tego ciągu ukazuje powyższy obraz. Aby otrzymać krzywą jak na rysunku z numerem 3, każdy z odcinków linii łamanej, zastępujemy czterema odcinkami trzykrotnie krótszymi, Granicą linii łamanych w ten sposób jest krzywa Kocha. Można pokazać,że przedstawiona krzywa w żadnym punkcie nie ma stycznych, a jej długość jest nieskończenie długa.
Zbiór Mandelbrota


Na zmiennej płaszczyżnie zespolonej rozpatrzymy ciąg, którego początkowy wyraz jest zerem. Pozostałe wyrazy są określone zależnością rekrutacyjną zn+1 = zn² + c. Podane we wzorze c jest parametrem zespolonym. W zależności od wartości parametru jest to ciąg algebraiczny, dążący do do nieskończoności, albo jest ograniczony. Wiemy, że jest to zbiór określony jako spójny, domknięty, ograniczony, posiadający niezwykle skomplikowany kształt.
Dywan Sierpińskiego

Przedstawiony na obrazie obok dywan Sierpińskiego, powstaje w następujący sposób. Podzielmy kwadrat na dziewięć jednakowych kwadratów i usuńmy wnętrze środkowego kwadratu. Tą samą czynność powtórzy z każdymi kolejnymi kwadratami, w wyniku czego powstanie 64 kwadraty. Z każdym kwadratem zrobimy to samo co na początku. To co pozostanie nazwane jest dywanem Sierpińskiego. Jest to domknięty i spójny zbiór. Każde dwa punkty możemy połączyć linią, która będzie całkowicie leżała w tym zbiorze. Jest on nigdzie gęsty i jego pole jest równe zero.

Animacja obok przedstawia kostkę Sierpińskiego.